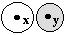College Mathematics: The Unteachable, Or Untaught?

by Ron Penner

I obtained a degree in Mathematics, so became somewhat familiar with the way it was taught and of the difficulties it seemed to engender in many others. These experiences prompted a series of problems which I later attempted to unravel, along with other related issues, which I now propose to explore.

I was often appalled and somewhat amazed at the manner in which these courses were taught, especially at the 100 and 200 level. There was so much verbage written on a blackboard or overhead projector which appeared to me to be pointless, albeit somewhat conventional. But later I began to muse, 'how can these subjects effectively be taught' and I began to appreciate the difficulties the professors experienced. I hypothesized that they had learnt and experienced Mathematics in a way far different from most of their students and that the gap was far too wide to be bridged by any conventional pedagogical methodology

What was this exprience of learning that they and many Math majors had and others did not seem to possess? The most basic was to regard this level of Mathematics, in most of its enormous diversity, as a language, a symbolic language that needed to be learnt and used. But it was much more sensitive to how much one took in at a glance, or alternatively how quickly one read that language, than learning to read one's native language, for this is much more akin to pattern recognition of an ungerlying logic, than to reading as it is usually understood. There seemed to me to be a minimum speed of assimilation that was requisite to fully grasp these concepts and courses, and that that was an aptitude that could hardly be taught. Another was an appreciation for the elegance of the reasoning entailed, and even the elegance of the notation. And finally, there was the ability and need, to generalize, to not be content with a theorem or lemma or definition until you had expanded these, until you had discovered as many of their extensions and further implications as possible. All of this was a mind-set that one either possessed or did not possess, although these are always matters of degree, but how does one teach a mind-set that is innate in some and absent in others? This is a very difficult question, and I am not sure that there really is an adequate answer to it.

I also found that I was very sensitive to the way such subjects were set forth on the page, and rummaged through the library until I found the most elegant text---seldom the one that was prescribed for the course. For if Bertrand Russell stated 'that there is no such thing as ugly Mathematics,' that did not preclude many ugly or less than elegant textbooks. And in the Physical Sciences, in particular, the ratio between written text or explanation and mathematical formulae was important to me, so that if one could follow the text simply by following the logical development of the mathematics, that always seemed something that was desirable. These I take to possibly be limited strategems to bridge the chasm I previously adumbrated. Of course, this dictum applies to any study, but particularly to Mathematics and to a slightly lesser extent the Physical Sciences, 'Never be content, initially, with the text that is assigned.' Then there is the appreciation of rigour of analysis. In an introductory course on Differential Equations, there was a text I always will value and esteem because it was so beautifully written and rigorous, which equated to greater simplicity and ease of comprehension. But one day I heard an acquaintance refer to this text as "the yellow peril"---it had a yellow cover---and that all of the students in his class detested it, and I was amazed and at a loss for words. Rigour of analysis, I mournfully concluded must not be an easily acquired taste. There is also the width of generalization of a particular approach which gives joy to that phenomena when it occurs. In trigonometry, the double and multiple angle formulae seem to bear no intimate relationship to one another. Then one discovers complex numbers and their utility, i.e. e to the i-theta power and the whole subject opens up and much greater vistas appear. I will always remember discovering, quite on my own, the Gamma and Beta Integrals. and the joy in discovering how many integrals could be fitted into these two basic structures simply through simple changes of variables.

But there are deep differences of aptitude and approach even among math majors themselves, perhaps greater than in any other discipline. There are those who excel in reading and comprehending and using the symbolisms, of which Algebra would be the prototype, and those who are far more spacially oriented, of which the Geometries serves as the prototype. I once heard of an experiment in teaching beginning college Mathematics at a private school for the gifted in Seattle. The material had been presented from an essentially algebraic prespective, when suddenly, in the middle of the course, it was taught from an essentially geometric perspective. And suddenly the class standing tipped over, becoming almost the exact opposite of what it had been. The geometric approach can greatly simplify many areas, but there are vast stretches of Mathematics for which there is no effective substitute for symbolic tranformations and manipulations. There is one further division which is the least recognized, but has increasingly become vital in more recent years. This involves a gift for, and love of, abstraction, for its own sake. This can also involve a love of getting at the fundaments of a subject. For lack of a better term, this might be called the Axiomatic Approach. Abstract Algebra can serve as its prototype and an n-dimensional cohomology group could serve as an example. Those gifted with this approach or aptitude will tend to have a better grasp of the whole of Mathematics, at least in outline form, and be the ones most likely to achieve some of the syntheses modern Mathematics desperately needs.

But I cannot leave this article so bleak and not attempt some remedies to the difficulties posed, some way of bridging these gaps for those not disposed to Mathematics in general. There are certain moments in the life of learning where one enters, in something approaching a Piagetian sense, a totally new domain. I believe one should, in many cases, pause and survey what lies ahead, emphasizing the great power and utility of the new approach, as well as some of the anticipated difficulties and how they may be overcome, rather than proceeding linearly to cover a prescribed curricula. One such branching point would surely be the point at which variables are first introduced to stand for any number within a specified domain. Also it might help if this introduction was combined with a sense that one was entering upon a new phase of mental maturity and growth. Then there are spectacular spurts in intellectual growth which can change and redirect one's whole life, and these need to be recognized and provided for. In his book, "Disturbing The Universe," Freeman Dyson briefly described an incident that occurred when he was ten years old. He purchased a book on the Differential and Integral Calculus about 700 pages in length, and when the family went for a winter retreat at Christmas break on the east coast of England just prior to World War II, he studied the work and did all of the problems for about ten hours a day, ten days to two weeks. I have always assumed since I read this, that if this or a similar experience had not occurred at about this stage, we would never have heard of Freeman Dyson. I had a similar experience, much later in life with the Calculus in an October retreat in Moclips---also on the ocean---after a summer as a forest lookout. The only way these experiences can be accomodated in colleges and universities, for those who need and are prone to them, in my opinion, is through a liberal, tutorial approach where one can design when and how to study a specific topic or field within a discipline. Someday psychometric tests may be devised to identify these individuals before they begin to enter college. But there are many instances in which courses tailored to specific disciplines such as Physics, Chemistry, the Life Siences and the Social Sciences are specially designed for the needs of these majors. This essentially involves applied Mathematics, in which a major aspect is to understand why certain formulae give a correct description of the phenomena they model, as well as how they can most effectively be used. This is far more than simply providing a list of relevant formulae and gives 'value added' rather than a 'cookbook approach.' And especially in the Social Sciences, Statistics must be taught to clearly delineate both the strenghs and limitations or various approaches. There is perhaps a great need for mathematicians to act as a kind of academic policeman and interfere in any department of the University when they feel that their subject is being misused or trivialized. But they must also, in such courses, teach others to---and demand that they--- think for themselves. They are not meant---and do not see themselves---as a service agency for the solution of problems in Mathematics, others in the university and society as a whole, find difficult to solve on their own. Finally, the Computer Sciences have taken over part of the former function of Mathematics in providing algorithms which encompass in their generality, almost all disciplines, and, in some sense, have replaced Mathematics, as the premier discipline for all of the other sciences---and this is wellcome.

My Senecan ramble must come to a close, hoping that it has not been too disjointed or too obvious.

Read More...

Summary only...

Basic Notions of Mathematical Proofs

by Frank Luger

Elementary mathematical proofs rest upon the basic principles of mathematical logic, which in turn are direct applications of classical Aristotelian logic to mathematics. Classical logic was used in Euclid’s Elements, on which all traditional geometry and mathematics was built, using propositional logic or the logic of propositions. The essence of propositional logic was laid down in the three famous “Laws of Thought” by Aristotle (384-322 B.C.E.), namely the Law of Identity (A = A), the Law of Non-Contradiction (A never equals non-A), and the Law of Excluded Middle (either A or non-A). They can also be expressed in symbolic logic as: if p, then p (p implies p by the Law of Identity); not both p and not-p [~(p and ~p), by the Law of Non-Contradiction, where the tilde ~ means negation]; and either p V ~p by the Law of Excluded Middle, where V means exclusive “or”. These ‘Laws of Thought’ have remained essentially unchanged ever since. In propositional logic, these basic principles take the following form (the Law of Identity is so basic that it is taken for granted, so it isn’t even mentioned): First Principle: Law of the Excluded Middle (for any proposition, p, the proposition, “either p or not-p” is true; Second Principle: Law of Contradiction (for any proposition, p, the proposition “p and not-p” is false); and the Third Principle: Law of Transitivity of Implication (for any propositions, p, q, r, the proposition, “if p implies q and q implies r, then p implies r,” is true. By definition, a general proposition is a proposition expressible in one of the following forms for a specific designation of x and y: (a) All x’s are y’s. (b) No x’s are y’s. (c) Some x’s are y’s. (d) Some x’s are not y’s. Propositions are many times stated in the form of hypotheses and conclusions. But one must be careful, because the conclusion being true provides no information in itself about the truth or falsity of the hypothesis.

There are certain relationships between implications involving the same two statements or their negatives that occur sufficiently often to make special terminology helpful, as follows. For a given implication, “p implies q”, or “if p then q” or “p only if q” is evident from what has been said above. The converse is the implication, “q implies p”, or “if q then p”, or “q only if p”’ while the inverse is the implication, “not-p implies not-q”, or “if not-p then not-q”, or “not-p only if not-q”. Finally, the contrapositive is the implication, “not-q implies not-p”, or “if not-q then not-p”, or “not-q only if not-p”. It is noteworthy that a given implication and its contrapositive are logically equivalent. The concept of logical equivalence applies in general to pairs of propositional forms. We say that two propositional forms are logically equivalent, provided they have the same set of meaningful values and the same set of truth values; that is, each has the same true-false classification as the other for all possible choices of the variables. For a true implication, “if p then q”, where p and q are propositional forms, p is said to be a sufficient condition for q, and q is said to be a necessary condition for p; i.e. q necessarily follows from p.

The purpose of the foregoings was introductory “warm-up” to enable us to apply logical principles to finding and proving new mathematical results. Mathematics is an abstract science in the sense that it consists of a system of undefined terms about which certain statements are assigned a true classification (these are the axioms and the postulates), which, together with basic defined terms, are used to develop additional propositions. These in turn, are then shown to be true or false according to the rules of logic that have so far been considered (such true propositions being called theorems).

Many of the new results in such a system are proved by direct methods that involve primary applications of the Law of Transitivity for Implications mentioned above.

However, indirect methods of proof are also used frequently, both in mathematical developments and in everyday reasoning, with compelling, even necessarily true results. When a child asks, “Has Daddy gone to work?” and Mother answers, “See if the car is in the garage,” it is likely that the thought pattern involves, “If Daddy has gone to work, then the car is gone.” When the child finds the car in the garage, he concludes, “If the car has not gone, then Daddy has not gone to work,” thus utilizing the contrapositive to arrive at a “No” answer to his original question.

Direct proofs both in their forward (reasoning from premises to conclusion) and backward (reasoning from conclusion to premises) varieties are quite straightforward, and as such, need not be treated here. However, while a direct proof may often be given where an indirect method is employed, the latter is often clearer, more forceful, and shorter. This is such an important phase of reasoning that it will be worthwhile to consider a general analysis and some further examples. There are essentially two forms in which indirect reasoning may appear, frequently interchangeably.

Form I of Indirect Reasoning consists of proving the contrapositive and thereby the desired implication. To show “p implies q” is true, we show that “not-q implies not-p” is true. For example, we assume simple properties of integers, also the definition that a prime number is a positive integer which is divisible by no other integers than itself and 1.

Proposition: If an integer greater than 2 is prime then it is an odd number.

Proof: (1) If an integer greater than 2 is not odd, it is even, by definition.
(2) If an integer greater than 2 is even, it is divisible by 2, by definition.
(3) If an integer greater than 2 is divisible by 2, it is not prime.
(4) Hence, if an integer greater than 2 is not odd, it is not prime, by the Transitive Property of Implications (vide supra).
(5) Therefore, if an integer greater than 2 is prime, then it is an odd number, since step 4 states the truth of the contrapositive.

Q.E.D.*

Form II of Indirect Reasoning essentially follows the pattern:
(a) To prove true: p implies q, where p has a true classification.
(b) Show: p and not-q imply r, where r is known to be false.
(c) A false conclusion indicates a false hypothesis; hence, not-q is false.
(d) Not-q being false shows that q is true. This is the desired result.

For example, assume the usual terminology of plane geometry and the proposition, “From a point not on a straight line, one perpendicular, and only one, can be drawn to the line. Prove the
Proposition: Two straight lines in the same plane perpendicular to the same line are parallel.

Notation: Let L be the given line through distinct points A and C, with AB perpendicular to L at A and CD perpendicular to L at C.

Restatement: If AB and CD are each perpendicular to L, then AB and CD are parallel.

Proof: Assume p: AB is perpendicular to L and CD is perpendicular to L, and not-q: AB and CD are not parallel.
(1) AB and CD not parallel imply that AB and CD intersect in a unique point P, by definition of parallel lines.
(2) AB and CD are distinct lines through point P not on L, both perpendicular to L, by hypothesis p.
(3) This is false by the proposition quoted for reference.
(4) Hence, not-q is false, since a false conclusion requires a false hypothesis in a true implication.
(5) Therefore, AB and CD are parallel (q is true).

Q.E.D.

Indirect methods of reasoning are sometimes called “proof by contradiction” (or reductio ad absurdum) due to the property of arriving at the negative, or contradiction, of a known true proposition. By virtue of the Laws of Thought cited above, (self) contradictions are absurd, and may therefore be safely discarded.

When the deductive aspect of inquiry, which has been emphasized above, is applied to mathematics or to other scientific fields, it frequently is preceded by an inductive aspect. The latter is concerned with the search for facts or information by observation and experimental procedure. Once the available facts have been assimilated, the scientist proceeds by induction to the formulation of a hypothesis or premise of a general nature to explain the particular facts observed and the relationships among them. The deductive aspect involves logical reasoning leading from this hypothesis to new statements or principles, which then may be checked against the facts already available. This use of inductive and deductive procedures to complement, reinforce, and check each other in the formulation of scientific knowledge comprises the main part of what is called the scientific method.

Note: Q.E.D. is a standard abbreviation from Latin, Quod Erat Demonstrandum (That which was to be Proved); but in the case of as yet unproven theorems, it reads Quod Est Demonstrandum (That which is to be Proved).

This is the Latin rendering of the original Greek phrases with which Euclid used to finish or start his proofs, and both of these have become habitual expressions in the classical mathematical literature of most countries.

Read More...

Summary only...

Erudition, Eloquence, and Elegance in Mathematics

by Frank Luger

In any field of human intellectual endeavor, the 'sine qua non' of 'eternal' excellence are the three classical hallmarks known as erudition, eloquence, and elegance. All these three, in turn, entail various qualities, as it will be mentioned below. They are the indispensable legs of the tripod on which true quality of the timeless transcendental kind rests, which may be best expressed by the single word: excellence.

Mathematics is a rather unique intellectual endeavor. Unquestionably one of the greatest triumphs of the human intellect -- and by the same token, a truly great tribute to it -- mathematics enables one to go 'where no one has gone before' or to borrow a literary phrase, 'where even angels fear to tread'. Now, in this essay, I don't wish to get drawn into such disputes as Platonic vs. Aristotelian mathematics, or whether mathematics is discovered or created or both; and I have no intention either to discourse on merits and shortcomings, or to engage in any kind of sermon for or against mathematics. Quite simply, the purpose of this paper is to draw attention to just what constitutes excellence in mathematics, regardless of the idiosyncrasies of any particular mathematician, whether still living or already standing in the Pantheon, frozen in lofty marble among eternal geniuses. In other words, don't expect here a cookbook recipe for winning the Fields Medal¹, quite regardless of how smart and (mathematically) knowledgeable you might be. You need much originality in this field, despite a huge amount of indispensable basic knowledge and rapid developments in every branch; and it is fair to say that no matter how impersonal mathematics appears, your own cognitive style and pattern-recognition gifts leave plenty of room for individuality in this special, infinite playground of the intellect.

However, none of the above justify the first sentence of the previous paragraph. Mathematics is unique because the man-made and the nature-made get intimately intertwined in it; and both components are present in every branch of mathematics, no matter where you look. But the proportions may be very different. In probability and statistics, number theory, and the like, the man-made aspect predominates so much that the nature made component can only be discerned with specific effort; whereas in most areas of mathematical physics, the nature-made aspect is not only conspicuous, but must even be given priority², at least according to the vast majority of (theoretical) physicists.

Also, there have been shifting emphases on these components throughout history; but it is only in relatively recent times, that mathematics has gradually become independent of natural philosophy at first and from physical significance at last. This emancipation has taken about a century, roughly between the non-Euclidean geometries of Gauss, Bolyai, and Lobachevsky in the early XIXth century until the Quantum Mechanics of Planck, Bohr, Schrödinger, Heisenberg, Born, Dirac, et al. around the 1930s. Dirac, in particular, in a famous quote has gone as far as asserting that if there is a discrepancy between experiment and mathematics, one ought to jettison the experiment and retain the mathematics. Today, maybe 10% or so of advanced mathematics has physical meaningfulness; and mathematical research merrily proliferates following its own recipes, in disdainful disregard of physics or even philosophy except perhaps for the part of philosophy which belongs to logic in general and mathematical logic in particular. In other words, the man-made component has become overwhelmingly, maybe to 90%, predominant over the nature-made component; and this is precisely why mathematics is so unique, considering that no matter where we look, it works.

A word of qualification is in order. It works, and ubiquitously at that; but this is still in our world of human sense-perception. How it may or may not work independently of the 'bubble' of virtual reality within which its human creators perforce live, remains an open question. If there is such thing as ultimate reality, it may or may not be adequately handled by our mathematical sophistication. One might conjecture, that human limitations can but result in projections of those limitations into other worlds, assuming that such worlds exist, quite independently of us. Also, with regards to extraterrestrial life, no matter how probable it is that such life is intelligent, there's no reason whatsoever, to suppose that those life-forms evolved intelligence along human lines. To be sure, there are certain mathematical things that we have reason to believe, are universal; for example the prime numbers, as it was eloquently emphasized in the late Cornell astrophysicist Carl Sagan's masterpiece: "Contact". But unless and until some way is found for interstellar communication and travel, we have no means to confirm or disconfirm such conjectures. Perhaps some future discovery will rob the 'Queen of Sciences' of her crown, but until then, mathematics reigns supreme, and we ought to bow to her.

Erudition is the first and perhaps most obviously important requirement for mathematical excellence. Little comment is needed. One must be intimately familiar with advanced mathematics in order to attain mastery. In fact, no attainment of mastery is possible before every detail has become so intuitively evident, that one can run circles around it and devise alternatives. It's just that the rapid growth of every branch of mathematics makes it increasingly difficult to master but ever narrower segments of specialities. A curious situation arises whereby the more one knows about specifics, the less one is able to keep sight of the whole, all the way until the absurd predicament of knowing everything about almost nothing. Already a hundred years ago this was well stated in one of Poincaré's theorems, according to which the more one approximates a mathematical truth, the more elusive it becomes. This recent proliferative trend has produced more and more 'specialist barbarians', which, of course, is at the expense of erudition, because erudition requires much general knowledge in addition to specialized competence in whatever narrow aspect of mathematics. This applies to both pure and applied fields of mathematics, although perhaps attains greater importance in the pure fields, because it is here that the specialization tendencies are the most pronounced. It is fair to say that today's mathematicians are less erudite in a general sense than ever, no matter how competent they may be in some highly specialized area. The only solution to this predicament is synthesis, whereby many seemingly disparate aspects are brought to common denominators; and the resultant simplification gives rise to generalization, which then makes room for new growth cycles. Generalization is one of the most important aspects of the growth of mathematics, being the key to usefulness. Interestingly, the greater the generality, the greater the simplicity. This is one of the main reasons why advanced mathematics is easier than the less advanced parts. Simplicity also greatly facilitates the other two requirements of mathematical excellence: eloquence and elegance, by getting rid of unwanted or unnecessary information and drawing attention to the important facts. Simplification by generalization was most eloquently illustrated by David Hilbert, the second 'Prince of Mathematicians' (the first was Gauss) in 1890, when he proved Gordan's 1868 theorem by throwing away 90% of Gordan's premisses and putting the rest into the form which is known as Hilbert's Finite Basis Theorem. This far-reaching and profound theorem shows eloquently and elegantly that greater generality and greater simplicity are practically inseparable.

Eloquence, as the second requirement for mathematical excellence, might strike a strange note. That's because eloquence is traditionally associated with rhetorics and the fluent, polished, and effective use of language, especially in public speaking. Yet the same argument or proof may be presented clumsily or eloquently. An eloquent proof immediately appears as smooth, almost natural flow of ideas, without even a trace of unnecessary or cluttering information. Obviously, a prerequisite of eloquence is thorough mastery of the field in general and the problem in question in particular. Yet, technical mastery is not enough. One needs a certain creativity and imaginative playfulness, as well as originality and style. This brings us to the third leg of the tripod: elegance.

Elegance, as the third requirement for mathematical excellence, is the truly artistic aspect. Its hallmarks are grace and refinement, ingenuity and simplicity, extraordinary effectiveness and efficiency. To explore, to discover patterns, to explain the significance of each pattern, to invent new patterns similar to those already known, are among the normal activities of what mathematicians do. How they do what they do depends on the quality of the mathematician. An excellent mathematician has an almost inimitable style, but despite much idiosyncrasy, the style will invariably be elegant.

The history of mathematics is marked by alternating contractions and expansions, analyses and syntheses, unifications and generalizations. If all of mathematical knowledge could be expressed in two principles, the excellent mathematician would not rest until s/he could demonstrate that the two are rooted in a single one. But that would give rise to new problems, and new cycles of expansions-contractions-expansions. Such pulsation has been characteristic of the growth of mathematics throughout history in erudite, eloquent, and elegant ways. As mathematics is both science and art³, it may perhaps be fairly said, that erudition stands for science, elegance for art, and eloquence bridges the two of them.

---

1 Equivalent of the Nobel Prize in mathematics, except that the Fields Medal is conferred upon its recipient only once every four years, in contrast to the Nobel laurels which are and have been awarded every year.

2 There have been many disputes around this point. Some famous people, such as Bohr, Dirac, etc. argued in favor of throwing out those parts of microphysics which 'deviated' significantly from mathematics; whereas Einstein et al. insisted on the priority of physics and the experimental validation of mathematical theories. Pure mathematicians in the vein of Gauss, Hilbert, Poincaré, Hardy, and many others, simply could not care less either way; for them the intrinsic esthetics and consistency of pure mathematics was far more important and normative than whether physicists happened to find any pragmatic use for beautiful mathematical theorems.

3 cf. Luger, F. Necessitas Mathematicae, in Commensal, No. 100, March 2000, pp. 20-24; also in Telicom, Vol. XV, No.1, Oct./Nov. 2000, pp. 66-71; Gift of Fire, Issue 122, Jan. /Feb. 2001, pp. 36-41; PhiSIGma, No. 23, Sept./Oct. 2001, pp. 20-25.

Read More...

Summary only...

Easy or Difficult?

by Albert Frank

Recently someone gave me the following problem:

On the Xth day of the Yth month of the year 1900+Z in the 20th century, a ship is near New York. The ship has T crew members, U propellers and V chimneys. If we add the cube root of the age of the captain (who is a grandfather) to the product XYZTUV, the result is 698823. What are the values of X, Y, Z, T, U, V, and what is the age of the captain? We also know that only one solution is realistic.

Is this problem difficult or easy? Let’s have a look at it (the solution):

The age of the captain (who is a grandfather) is a perfect cube: It can only be 64 years old.

698823 – 4 = 698819.

Let’s make a decomposition of 698819 into prime factors: 698819 = 11 x 17 x 37 x 101. We have four factors. Six are needed, so the two others are 1 and 1.

11 would be a too big a number for propellers or chimneys, so the ship has 1 propeller and 1 chimney.

The month has to be <13, so it can only be 11.

The day has to be < 32, so can only be 17.

The year (Z) has to be < 100, so can only be 37.

The remaining number 101 is the number of crew members.

We have it: 17th November 1937, 1 propeller, 1 chimney, 101 crew members, and the captain is 64 years old.

Some will find this problem very easy, others will find it very difficult.

Read More...

Summary only...

Complete Fools

by Richard May (Not an np-complete fool.)

Do there exist some complete fools who can not be proven within any given deductive system to be complete fools, as a consequence of Goedel's Incompleteness Theorem?

Does Godel's Incompleteness Theorem apply to complete fools?

May-Tzu

Read More...

Summary only...

Dialogue Involving A Question of Statistics

by Fred Vaughan

"I've got a question, Ray. Everyone knows your opinions about miracles and that it's all physics, so what I want to know is how your good fortune can be reconciled with statistical probabilities. What you have experienced seems impossible to me, Ray!"

"It's the wrong use of the telescope again, Tim."

Tim listened and laughed. "How can that be? Where's the telescope?"

"Well, you're asking about the probability of an event after it has already occurred, aren't you? So probability and statistics don't apply. Statistics has to be directed the other way. Let's say I flip a fair coin one hundred times and get one hundred heads in a row. How would one square that with statistics? Isn't that the essence of your question?"

"Yes! That is the question, Ray! How is it you could flip one hundred heads in a row?" Tim affirmed.

"Well, what if I had flipped a head and a tail alternating until I had fifty heads and fifty tails? Would that bother you as much?" Ray asked.

"No, of course not! That's fifty-fifty, right on the law of averages!" Tim said.

"Well, you're using your telescope incorrectly then, because both cases — a hundred heads in a row, and a sequence of head-then-tail fifty times in a row — have exactly the same likelihood. The only reason you think the one case more likely is because it's similar to a kazillion other cases that are also fifty-fifty. But whatever combination of heads and tails that you get after a hundred flips of that coin will be exactly the same likelihood as the hundred heads, Tim. You flip a coin a hundred times and whatever sequence of heads and tails that you get will have been exactly that unlikely. But a lot of them are disguised."

" Disguised? You've got to be kidding me, Ray!" Tim was not convinced.

"Nope. I'm not." Ray seemed to be done with that discussion.

Tim came back with, "Wait, Ray! That makes no sense! This kind of thing just doesn't happen!"

Ray seemed somewhat tired as he replied, "Your key phrase there was 'kind of thing', Tim. Classes of situations like flipping fifty heads in one hundred flips of a fair coin are the 'kind of thing' that are phenomenally more likely than flipping all heads or all tails. But what you're missing here is that each one of those situations like, head-tail-tail-tail-head-head-tail-head… etc., is no more likely than flipping all heads. There are just more situations that comprise the class involving fifty heads. There are kazillions of them like I said. Does ten-to-the-twenty-ninth have any meaning for you, Tim? Remember! Whenever something actually happens, it is a single situation not a class of them. Everything is unlikely, Tim. Everything! When you flip your coin a hundred times, whatever you come up with will have defied odds of ten-to-the-thirty-first-to-one! But don't doubt for a second whether what happened actually happened, or if it defied the laws of physics, just because of that or you'll be legally insane. Something happens! It has to."

Tim looked as baffled as an ostrich blinking at a bright sun.

Ray knew he had been a pompous asshole. He had indeed been phenomenally lucky. He had to admit that much. Wasn't 'fair' coin defined as one for which one hundred heads in a row does not happen? What about each subsequent flip of that coin along the way? Any one of those coming up tails would have terminated the phenomena of Ray Bonn. Ray Bonn was not some metaphysical being standing back behind a protective glass watching the coin flipping; he was the coin flipping. He was the outcome of all the contingent coin tosses; anything else was an instance of that most major of logical fallacies, looking down the wrong end of telescopes.

Read More...

Summary only...

The Statistics of Stereotyping

by Fred Vaughan

In Albert Frank's article "The Interpretation of Statistical Tests" he provides formulas and examples of the errors one can get into when applying a test of a known high reliability to determine whether subjects taken at random qualify as members of a select (generally a negatively perceived) group. This is the problem with "racial profiling" that was identified by "Renaissance" in his posted comment which many fail to understand properly.

Let us take as a given that a particular racial type that is readily identifiable happens to be represented at a much higher incidence frequency in some sort of crime or other. This could be theft, murder, terrorism, or whatever statistics provide convincing "justification." And let us suppose further that the statistics that are used are completely valid such that, for example, although one race constitutes only 10% of the total population, its members who perpetrate said crime outnumber those of the majority racial type who also perpetrate such crimes. Why would profiling in such cases be unwarranted even (or especially) from a mathematical perspective?

Here's why.

Suppose that there is a test in place that can be applied to individuals that is extremely reliable (defined as f as in the original article) with regard to determining the culpability of an individual having already committed (or who will in the future commit) said crime. There is nothing in the justification statement given above that has any direct bearing on the appropriateness of implementing such a program. Although those may be completely valid statistics, they are not sufficient to determine the efficacy of a program which they attempt to justify. The appropriate statistic is "what is the probability that an individual of the subject race may commit such a crime — the parameter a in Albert Frank's article. This number will always be small — much much smaller than the probability of an individual having already committed the crime being a member of the subject race. This may seem like a subtle difference, but it is not!

Suppose the racial mix of a population is only 10% A and 90% B and that some precentage a_a of those who commit crime C are from the subset A. So far we have nothing to go on. We need to know the percentage of the entire population who commit crime C. Let c be that probability. Then we can determine the likelihood of a member of A or B comitting that crime. If we define a and b as the probabilities that members of A and B will, respectively, commit the crime, we can then solve the problem using what we know as follows:

a * (0.1) + b * (0.9) = c, and

a * (0.1) / c = a_a

Given a_a(which is usually all that is given and that is usually insinuated as though it were a itself — which it is not), and one of the following, a, b, or c, we can determine the effectiveness of profiling for a given reliability of testing.

Let's say by way of example that one in a thousand (c = 0.1%) of the total population commit the crime. Then for a_a= 0.6 we would have:

a = a_a / 100 = 0.006 and b = ( 0.01 − 0.1 * a ) / 0.9 = 0.00044.

Since in racial profiling the population is effectively reduced to that of A rather than the much larger A + B, it is a (as defined here) that corresponds to the same term in Albert Frank's article. So in order to avoid the use of profiling producing law enforcement nonsense, the reliability of testing an individual once he is subject to test must be so good that 1 − f would be much less than 0.006 or there will be as many or more unlawful (false positive) arrests as lawful ones. And in law enforcement a reliability as high as even 0.9 (let alone the required 0.994) is unheard of!

Therefore quite aside from the issue of the impertinence of the practice, it is a very ineffective approach to fighting crime.

Doodles in Author's Anthropology Class Notes from 1962

Read More...

Summary only...

Spinors

by Martin Hunt

A photograph of a lithograph produced by Martin Hunt.

Read More...

Summary only...

So Much For Everything, then!

by Ed Rehmus

Leonhard Euler, a Swiss mathematician of the 18th Century who was clever enough to point out that the fundamental logarithmic number e multiplied by itself the square root of minus one time(s), and that then multiplied by itself 3.14159265... times cannot be saved from non-existence by the addition of one, but at least is nothing less than zero. This is clever because the formula successfully contains all five fundamental numbers (0, 1, π, e and i).

Leonhard Euler

Even less relevant, however, was his announce-ment to the atheist Denis Diderot, "Sir, (a+b)ⁿ/ n = x, hence God exists!" Since Diderot was not a mathe-matician he was totally bumfuzzled by that. But since Euler went on to challenge the atheist, "what do you say to that?" Leonhard obviously must have had more to say than that the sum of any two known rational numbers to some power (presumably not zero) and then divided by that power will equal some unknown number. Unfortunately, since Diderot fled the scene red-faced and bladder-emptied by this puffball, the ultimate proof of God's existence remains untransmitted to us.

Although mathematics is probably the most thorough-going of all man's anthropomorphic pursuits, it still cannot break free of anthropomorphism itself. It uses a symbolically human abstraction of human logic to prove purely human questions and to set the parameters of purely human quests. Since we cannot understand any intelligence higher than our own we can never properly evaluate the limits of our confinement nor its priority in the cosmic ladder.

There are yet a few wisemen of the tribe, mirabile dictu, who insist that things are just as wonderful as they have always been. Isn't motherhood still the purpose of existence? Dubya may have his faults, but he is still our president, isn't he? Global warming will help us cut down on our fuel bills, won't it? Why do I need Medicare if I never get sick? Amidst such incontrovertible axioms, Euler's incandescent formula sends rays of glaring irrelevance over the whole meaningless night of Panglossian optimism.

But now into this darkness comes a devastating, heart-stabbing news flash from current astronomy that the universe is about to become even darker. For the universe is not merely expanding in every direction, but said expansion is growing faster and faster by the nanosecond. Within a relatively short time we shall have blown far outside the range of all the stars to find ourselves spinning alone and silent in empty space. Solipsism seems not only the province of anthropism but is apparently the irrational, if not downright nonsensical, predilection of astrophysics as well.

You might well ask, what virus it is that causes a cell to explode. Then maybe some 21st Century Euler could measure the velocity thereof, provided of course he was able to decide whether to use a microcosmic, macrocosmic or anthropocosmic hourglass.

Read More...

Summary only...

The Interpretation Of Statistical Tests

by Albert Frank

In this article, we assume the following hypothesis: if the reliability of a dichotomical test is f, then the probability that it gives a wrong result is 1-f.

The following question arises: Below what reliability will a test result have a probability of being correct of less than 0.5?

Let P be the number of elements in the population, a the probability (known) for an element of this population to have a definite feature K, and f the reliability of the test. The number of K-elements detected by the test equals a f P. The number of non-K detected (wrongly) is (1-a) (1-f) P. The probability that an element detected by the test is effectively a K-element is 0.5 if a f P = (1-a) (1-f) P, equivalent to f = 1-a. So, as soon as f ≤ a, the test becomes a nonsense.

A test must be more reliable if what it attempts to detect is very rare.

This simple fact is very often neglected.

Let's take an example: the alcohol test. We assume as hypothesis that one driver out of 100 is at "0.8 or more" (European norm for heavy offence is in excess of 0.8 gm/ltr.). In the following table, we examine for several reliabilities of the test the probability that somebody with a positive test is actually positive. We take a population of 100,000 persons, of which 1,000 are supposed to be "at 0.8 or more."

Reliability of the test	Valid detections	Invalid detections	Probability a "detection" is valid
.9999	1,000	10	0.99
.999	999	99	0.91
.99	990	990	0.50
.95	950	4,950	0.16
.9	900	9,900	0.08
.8	800	19,800	0.04

We can imagine the dangers of bad interpretations of tests in, for example, the medical field.

Read More...

Summary only...

The Organization of Sensory Experience into Sensory Spaces and Their Coordination with Physical Space

by Huntley Ingalls

Abstract

Visual, kinesthetic, and tactual sensory fields, visual afterimages, and dreams have spatial characteristics, although physical space is commonly considered to be the only real space. Characteristics of non-physical spaces will be described using the concept of sensory spaces, which was introduced by the French mathematician Henri Poincaré at the beginning of the twentieth century. Poincaré argued that space should not be conceived of as an immutable medium containing objects and events, but as a field of operations that is supported by a variety of processes and operations and the laws by which they succeed one another. The coordination of sensory spaces with physical space will be discussed by approaching the idea of space through the mathematical concept of a manifold--an idea more fundamental than space, which is a type of manifold. This approach facilitates a deeper understanding of the nature of spaces, the ways in which spaces are generated, and how sensory and dream spaces have extension that does not conflict with the extension of physical space.

Visual, tactual, and kinesthetic sensory experiences, visual afterimages, and dreams have distinct spatial characteristics. The relation of these spaces to physical space is a difficult issue in the philosophy of perception. How can sensory images and dreams have spatial features and how can such spaces coexist with physical space, which is commonly assumed to be the only real space? Clear insights into these difficulties are possible through ideas on the nature of space that have been developed by intensive geometrical research in the last 150 years. A favorable ground for pursuing these ideas can be prepared by considering the development of spatial concepts and operations in children or congenitally blind people whose sight has been restored by surgery. This can relieve the constraints of mistaken attitudes and preconceptions about the nature of space that make confusion almost inevitable.

Piaget's research shows that the child's concept of space begins with an almost undifferentiated flux and is built up through several very definite and revealing stages.¹These stages include: the recognition of certain constant combinations of features and patterns; the ability to follow a moving object and recognize the invariance of its form despite its movement; the understanding that an operation, such as hiding an object, can be undone by a second operation; and the child's discovery that he can go from A to B by many paths, and if this is done by any one path he can undo it by many alternate paths. At the end of these stages the child acquires a mental map of the world with a set of permanent places occupied by various objects, one of which is himself from which there is a unique perspective on the world. Later these concepts of space are extended to the refinements of perspective, topological relationships, and geometrical thought. This map pervades perception so intimately that it seems to be an inevitable and necessary feature of experience, and it becomes nearly impossible to question its basic nature.

Congenitally blind people whose sight has been restored by surgery experience great difficulty perceiving three-dimensional space and the relations between objects. They are able to see little at first, and cannot name objects or distinguish between simple objects and shapes. The visual field is a confused pattern of light, dark, colored, and moving visual sensations that bear little resemblance to the visual field of a normal person. They tend to see only the outlines of solid geometrical figures; for example, a sphere appears to be the same as a disk. There is usually a long period of learning before the formerly blind can develop useful vision, and in some cases this is never accomplished. Some give up the attempt and revert to a life of blindness, often after a period of severe emotional distress. Some quickly learn to see rather well; particularly those who are intelligent, active, and who have received a good education while blind. One of these, a man who had been blind from the ages of 10 months to 52 years, enjoyed making things with simple tools and longed for a time when he might see. He tried throughout his life to picture the visual world. When his bandages were removed he did not suddenly see the world of objects as a normal person does. He was able to use his eyes well after a few days and judge distances and sizes accurately if he already knew a particular object by touch, although his sense of vertical distance was much distorted. He was unable to recognize objects that he had not touched and was unable to draw anything he did not already know by touch. His tactual and kinesthetic experience had enabled him to develop a sense of space which, after some effort, could be transferred to his newly acquired vision.²This research confirms the ideas of the French mathematician Henri Poincaré, who wrote in the early twentieth century that isolated sensations cannot provide an individual with a concept of space; rather, this is developed through learning the laws by which these sensations succeed one another, especially in response to the voluntary movements of the individual.³Space is a concept that is abstracted from physical operations, and not a static medium containing objects.

The concept of sensory spaces becomes more accessible through the mathematical idea of a manifold. The concept of a manifold is more general than that of space, which is a subset of manifolds. It enables us to develop basic ideas that are fundamental to the concept of space. Since the idea of a manifold is more abstract and unfamiliar than that of space, we do not approach it with the same ingrained attitudes we have about space. This enables us to bypass some of our preconceptions and permits a fresh and powerful perspective on the concept of space.

Manifolds

The location of any book in a bookcase can be specified by two descriptions; for example, third shelf from the top, eighth book from the left. The location of any bead in a string of beads can be specified by a single description, such as eleventh bead from the left. A manifold is any set of elements such that the location of any element in the set is completely specified when all of n essential descriptions are given. The elements may be objects, operations, or anything specifiable, and the description may be any clearly defined characteristic that is variable, such as distance, brightness, or weight. A manifold is connected if for any two of its elements there exists a chain or path between them such that every element of the path is a member of the manifold. The string of beads is connected; the shelved books are not because there is no path of books between the shelves. A connected manifold is discrete if a passage along a path in the manifold encounters abrupt changes in the varying characteristics; otherwise it is continuous. For example, movement along a string of beads, or through a series of Morse code sounds, encounters sudden changes between the elements. The colors of the spectrum, or the muscular sensations of extending an arm, form a continuous series of gradations into other colors or muscular sensations.

A manifold is one-dimensional if the removal of a single element divides it into two parts such that there is no unbroken path between the parts. A manifold is two-dimensional if the removal of a one-dimensional manifold divides it in a similar manner. It is n-dimensional if it is necessary to remove an (n-I)-dimensional manifold in order to divide it.⁴For example, a succession of musical notes of continuously varying pitch is a one-dimensional manifold, because the removal of a note in the succession makes any passage through it encounter a sudden jump in pitch. If each note can be sounded with both varying pitch and intensity, two descriptions are necessary to specify a sound, and we now have a two-dimensional manifold. The removal of a single note will not cut it into two parts. A one-dimensional manifold must be removed; for example, all notes at middle C in all its intensities. Any path between notes less than and greater than the removed pitch would encounter a sudden jump. Similarly, each note may be varied in tone to form a three-dimensional manifold.⁵

Continuous connected manifolds are very common in ordinary life. The shades of gray between black and white, and the spectrum of weights between two given weights are one-dimensional manifolds.⁶The color continuum is a three-dimensional manifold of hue, saturation, and brightness. A sensory manifold is any manifold that depends on the stimulation of a definite set of sense organs in a particular individual. The sensory manifolds are especially significant for the idea of sensory spaces.

Suppose a person is blindfolded and his skin touched with two pin points. That person can distinguish between the points if there is sufficient spread between them, but when they are brought together they are felt as one point. From any tactual point on the skin there is a path of such points to any other tactual point on the skin; that is, there exists a one-dimensional manifold of tactual points between any two such points on the skin. Now consider a continuous series of such points encircling the arm, and then imagine that they have been removed. All the tactual points have now been divided into two distinct domains, the points that are on the lower arm and those on the rest of the body. All paths between points in these two areas are broken by the series that was removed. It is necessary to remove a one-dimensional manifold of tactual points from the skin in order to divide it into two separate domains of tactual points. The set of all tactual points on the body is a two-dimensional sensory manifold.

Visual manifolds are more complex. The basic visual field is two-dimensional. Visual elements are directly perceived to the right and left and above and below the direction of sight. Objects are also perceived at various distances from the eyes, but this third dimension of the visual field does not have the simple direct quality of the other two. Otherwise, the far side of opaque objects would be visible. The visual elements are assigned distance values according to a complex set of cues, such as muscular accommodation in the eye, hue, brightness, superposition, perspective, and texture-density gradients. The visual elements are distributed in a two-dimensional field, but the cues assign a third characteristic to the elements which makes the visual experience a three-dimensional field. Turning the head or walking generates a continuous family of visual fields which are integrated into a single system. Such activity adds parallax shift, which is an additional distance cue. The family of visual fields arising from the observer's movements and past experiences is integrated into a common manifold. The various descriptions specifying the location of elements in this integrated family of visual fields can always be reduced to three independent descriptions.

The set of feelings that corresponds to the various stages of contraction of a muscle is a one-dimensional manifold. All of the families of muscular sensations are integrated into a common three-dimensional kinesthetic manifold. Two different kinds of sensory manifolds can be combined into a common manifold, and the equivalence values between the two kinds of sensory elements reduce its dimensionality. For example, vision and the handling of objects are coordinated into a visual-kinesthetic manifold. When one reaches for an object, the hand is seen to touch it exactly when the arm is felt to be sufficiently extended. No more than three descriptions, visual or kinesthetic, are needed to specify any element of this system. For example, the location of an object may be described by saying "Walk thirty paces forward, then fifty paces to the left, then look up eight feet."The system is further elaborated by incorporating values from other senses, such as tactual and auditory ones. All the senses are integrated into a three-dimensional general sensory manifold.

Spaces

Connected manifolds are the essence of space. Understanding space through this concept provides a perspective of its basic nature that is free of misleading preconceptions. A space is a connected manifold such that each element has associated with it subsets of elements called neighborhoods. A neighborhood may be thought of loosely as a region of elements having the same general properties as the manifold. For example, any small region on the surface of a sheet of paper is a two-dimensional manifold similar to the two-dimensional manifold of the entire sheet. The elements are called points, and the kind of space depends on the particular axioms that the neighborhoods satisfy. The most familiar spaces, when idealized, satisfy the following conditions:

1. Each point has at least one neighborhood.
2. Any two neighborhoods of the same point have a common subset, which is a neighborhood of that point.
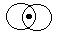
3. If the point y is contained in a neighborhood of the point x, there exists a neighborhood of y, which is a subset of the neighborhood of x.
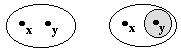
4. For any two distinct points there exist two neighborhoods without common points.

The familiar space of normal life satisfies these conditions. Visual, tactual, and kinesthetic manifolds are less stable,⁷Yet, as they are experienced, they generally satisfy these axioms and are sensory spaces. We have seen that the sensory manifolds are integrated into a more complex manifold of sensations, memories, and abstract manifolds to form a more stable general sensory manifold. This manifold satisfies the axioms more consistently, and it is a space.

The neighborhood axioms outline the connectivity properties of a space, that is, their topology. A metric space is a space in which all pairs of points have a well-defined distance relation.⁸For example, the separation of any two points in the space of a room may be expressed in centimeters.

Consider an extended one-dimensional space whose elements are points of light consecutively ordered by increasing brightness. Each element is uniquely situated in the space by its brightness specification, but it is not necessary to designate a brightness value in order to locate an element uniquely. The nth brightness is also simply the nth element. A position can be associated with every element of the space, and the set of all positions is itself a space. Such second order spaces can be associated with primary spaces of any dimensionality, and the corresponding spaces have identical mathematical characteristics. We can think of such abstract spaces as background for the primary elements. This provides us a powerful basic system as a reference for the primary elements. The background space is abstracted from the primary elements and their relations. They can no more stand alone than the current of a river can flow without water, although it is very expedient to work with the abstract properties of spaces as with purely mathematical hydrodynamics. In the sensory spaces we have an operational awareness of both primary elements and abstract positions. The general sensory manifold is a very complex unity of concrete and abstract spaces.

The operational experiences of ordinary life support a concept of universal space that incorporates all the sensory spaces into a general frame of reference for the familiar world. This is what is thought of as public or physical space. It is the space referenced in describing places, shapes, and locations to other people. Physical space has many advantages over sensory space. It is not centered in the individual. It incorporates a lifetime of experienced sensory spaces and includes the ground of possible sensory spaces that have not been experienced. It is far more consistent and dependable than sensory spaces. Unlike sensory spaces it is homogeneous and isotropic.⁹A very important characteristic of physical space is represented by the postulate that the interval between any two points on a rigid rod remains independent of any motion of the rod, thus enabling consistent measurements.

This line of development is continued in geometry by considering a mathematical space that is an idealization of physical space. It is then possible to study the purely logical properties of this ideal space. While Euclidean geometry appears to represent physical space quite well, mathematicians have constructed other internally consistent spaces. It is possible that some non­Euclidean geometry could be a better model of the physical universe on a cosmological scale. Pure mathematicians even postulate spaces that have no relation to the physical world. They are concerned only with the purely mathematical properties of these ideal constructions.

Physical space and time are commonly thought of as systems of infinitesimal points and instants, but these are concepts of ideal mathematical space and time. Empirical spaces differ from such ideal spaces. A person's vision has a lower limit of acuity, although there is no awareness of the grain of the visual field. The cell assemblies that operate as functional units in the retina, lateral geniculate body, and visual cortex suggests that the sensory fields do not function in the same manner as operations performed on isolated independent points. The operational elements of the sensory fields are not the momentary elementary sensations described by the

structuralists, but are entities such as line segments, corners, or vowels, which reflect the pattern of neural operations. Infinitesimal points and instants are essential concepts in the mathematical analysis of the ideal spaces of geometry and physics, but they are misleading for sensory spaces. Physicists have considered the possibility that even physical space and time are not composed of infinitesimal elements.

Human perceptions do not arise from operations on points of from momentary sensations. An overall structure is built up and abstracted from looser and more expanded elements, from which points and instants can then be constructed. The smallest elements common to the overlapping of the operational units of sensory space define its points. These natural units can then be redefined in terms of points. Thus, the operational priority of the units becomes replaced by the structural priority of points, which misleadingly suggests that points have operational priority. Isolated sensations are not elementary experiences. However, ideal concepts have mistakenly led to the structuralist school of perception.

One of the features most intimately associated with the familiar space of ordinary life is extension. Extension is not the same as distance. Time is not extended in the manner of space, yet it satisfies the conditions of the distance relation. Extension is regarded as such a universal and convincing characteristic of the space of human experience that it is considered to pervade throughout the world and encompass all of existence. This belief is problematic in the philosophy of perception, and makes it necessary to understand the nature of extension and its implications for sensory spaces.

A space is extended if it satisfies the following conditions:

1. All pairs of elements have separation; this is the last of the four neighborhood axioms.
2. All elements exist simultaneously.
3. For any two elements, and any path within the space connecting them, there is a possible operation for traversing that path by a movement that acquires the specifications of each element as it is encountered.

The first condition is the basis of the idea of "here," "there," and "a partness." The second condition is partially the basis for the strong feeling of reality and stability associated with ordinary space. From the vantage point of any part of an extended space, other parts are considered to be there now. The third condition provides the feeling of access, in principle, to all parts of an extended space. These conditions are not only satisfied by physical space, but also by the visual, tactual, and kinesthetic fields and by general sensory space.

A series of objects of continuously increasing weight has separation and simultaneity, but there is no movement from one weight to another that acquires the varying weights. There can be the implied movement that results from changes in attention, but attention is not the same as weight.

Voluntary movements are critical to the development of the concept of extended space because access, in principle, is a fundamental feature of such space. Thus the kinesthetic manifold is a uniquely important subspace of the general sensory manifold. One can directly control and change separate parts of kinesthetic space at will, allowing an ease of direct access to all its parts unmatched by the space of other senses. This feature generates a feeling of being a part of physical space while the other senses provide a feeling of observing it. In kinesthetic perception an object can actually be surrounded by a system of muscular movements. The object then appears to be embedded in a space generated by the movements of the body. This special characteristic of kinesthetic space is incorporated into general sensory space which is then generalized into physical space.

The imagery in dreams that are clear not only satisfies the criteria for space, but also for extended space. Dream spaces are usually extended in three dimensions, with separation, simultaneity, and voluntary movement among the elements. The philosopher H.H. Price described the spatial relations of dream images in vivid language:

If I dream of a tiger, my tiger-image has extension and shape. The dark stripes have spatial relations to the yellow parts, and to each other; the nose has a spatial relation to the tail. Again, the tiger-image as a whole may have spatial relations to another image in my dream, for example to an image resembling a palm tree.¹⁰

It is common in dreams for a person to walk down a path, cross a bridge, see a face, look into a canyon, or approach some object of interest, all of which are spatial experiences in the dream.

Physical space is commonly regarded as a unique medium in which all of existence is embedded. This implies that there can be no extended spaces other than physical space, and hence that dream and sensory spaces are unreal or paradoxical. The imagery in dreams has extension, yet the extension of a dream space cannot be extension in physical space. This paradox is resolved by the realization that space is nothing more than a special kind of organization of elements. A system of elements may be a space under the organization of one domain, but not a space when viewed through the organization of a different domain. The source of a dream space is neural events occurring in physical space, but the geometric relations in dream space are not geometric relations in physical space. A pair of independent radiophoto transmissions occurs in the same space from the viewpoint of the physical world, but there are two image spaces from the viewpoint of the organizations within the signal variations. There is a basis in physical space for the image spaces, but that basis is only a play of signal variations when viewed within the geometry of physical space. What is space from one organizational vantage point may be only a collection of disordered elements from another. Thus it is possible that dreams and drug visions, which are extended spaces, can have an electrochemical basis in the brain and yet be completely unrecognizable as images and spaces from an ordinary physical point of view.

Extension in dreams does not conflict with the extension of physical space, because the elements and operations in dreams are not a recognizable submanifold of physical space. A dream manifold is not merely a simulation of extension. The third dimension supported by perspective and other cues in a painting is a simulation of extension, because there can be no access movement in that dimension except through changes in attention. There is motion in the third dimension in a movie, but there is no way for that motion to be accessible. It is possible to control movement in the third dimension of a mirror, but the source of that control is not within the image space. The image space is extended in a third dimension in accordance with the image behavior, but the source of movement is not in that space. Dream spaces are usually extended in three dimensions, but sometimes only in two, and there is separation, simultaneity, and voluntary movement among the elements. Unlike the case of images in a mirror, in a dream the source of movement is within the space. The visual, tactual, kinesthetic, and general sensory spaces also have genuine extension, and their association with physical space is sufficiently close to support the common attitude that those extensions are somehow part of the extension of physical space. Approaching the concept of space by means of the idea of manifolds clearly shows how it is possible for spaces to exist within spaces, that have no common organization except from a perspective outside the system.

The idea that the familiar extended space of ordinary experience is generated by events and is not a unique and eternal medium in which objects are immersed is startling to common sense. The complex of sensory and physical spaces and their second-order fields, which are ordinarily termed "space," has such a comprehensive framework that it is difficult to show that space is not an immutable medium without implicitly assuming such a medium. Our spatial framework is so constantly present and familiar that when we attempt to imagine it in the absence of operations_, a second order field remains before us and we speak of "empty space." But that space is not truly empty. We have subtly intruded unconscious attitudes into it, which support that space. Thus space is usually construed to be an absolute entity. Liebnitz thought of space as "an order of coexistences"but this idea was two hundred years ahead of its time.

Generation of Sensory Spaces

The mutability of the sensory spaces is more readily apparent. Tactile space is abolished when the body is immersed in water at body temperature and sensation is nullified. When all muscular activity ceases, the kinesthetic space of the moment is nothing more than rather vague attitudes associated with previous muscular experience, and thus it is clear that kinesthetic space is entirely dependent on muscular activity. It becomes clear that the third dimension of visual space is generated, when we perceive the effects of altering basic depth cues by optical instruments or reversed lighting. A different three-dimensional space is then experienced, which may have exaggerated depth, be stretched out, or reversed. When a person first wears new eyeglasses, his visual and kinesthetic coordination are initially upset. The street may look closer than his sensations indicate. His general sensory space is distorted by altered correlations until he is able to learn a new system. The basic two-dimensional field is never absent in the waking state, but the deterioration of acuity toward the edges of the field and the phenomenon of the blind spot reveal that it is generated.

Physical space is less mutable than general sensory space, yet modern physics has shown that physical space is not independent of physical processes. It is distorted under the extreme conditions considered by relativity theory. The geometric properties of physical space are determined by matter and its transformations.

Some sensory spaces have the character of a medium, which is any definite kind of entity distributed in the manner of an extended space. A painting is supported by the medium of paint. The momentary visual field is the medium of visual sensations. Kinesthetic space is not a medium, because its extension is supported not by muscular sensations alone but by those sensations and attitudes about possible muscular sensations. General sensory space is a fabric of sensory media, operations, and attitudes. Physical space is a manifold of physical transformations and their second order spaces. Physical space is not a medium, but our means of conceptualizing it subtly projects it on imaginary media. The visual field is a very strong source of this projection. The tendency to think of physical space as a kind of nothingness which is yet a medium contributes to the confusion felt when we try to imagine the limits of a finite physical universe. None of the higher-order spaces is a medium, because the elements have only mathematical properties.

Spaces have no independent substance of their own. All are dependent in various ways on first-order elements and their relations. The main difference between the spatiality of sensations and that of objects is the degree of refinement to which metrics can be assigned to them. Ideas of physical space are developed by means of experiences with physical entities. As Poincaré observed, the body is a crude measuring instrument, and the instruments that the child owes to nature and those the scientist owes to his ingenuity have the same fundamental basis in the solid body and the light ray.¹¹Physical space has no properties independent of the instruments used to measure it, and to geometrize is to study their properties.

The familiar extended spaces have a smooth contiguity from region to region that appears to be one of their immutable features. Yet the visual field has a lower limit of acuity, although we are not aware of boundaries or gaps between the visual elements. Direct scrutiny of the visual field is incapable of detecting them because they do not exist for that operation, just as one cannot feel the roughness between the grains of sandpaper. Any operation that traverses a set of elements in such a way that gaps are undetectable has a smooth continuity for that operation.¹²A time lapse movie of a door in which each frame shows only a closed door may have gaps in which the door is open, but that will be completely invisible in the film and only a smooth continuous sequence of a closed door will be apparent. Areas that are contiguous in one operation may not be with respect to another. It is possible to construct a set of contiguous areas on a flat surface which are in separate planes situated at various distances when viewed in a stereoscope.

The Pulfrich pendulum illusion is an elegant demonstration of the neural system's ability to generate space. Cover one eye with a dark transparent glass and let a pendulum that consists of a weight and a string several feet long swing in a straight arc perpendicular to the line of sight. When the oscillating bob is viewed with both eyes, it appears to circumscribe an ellipse. The eye that is adapted to the dark takes a longer time to integrate energy and send messages to the brain; hence it sees the bob slightly in the past. The disparity in the effective position of the two eyes generates an ellipse which the bob appears to trace in its swings. The time discrepancy is equivalent to a binocular parallax effect which, for the brain, is exactly as if the bob were really swinging in an ellipse. Julasz's random dot stereograms create another effect that vividly demonstrates the ability of the central nervous system to generate space. These are special pairs of displays constructed with a computer in such a way that each display consists of random dots with no recognizable structure, but when viewed stereoscopically they are perceived as a geometrical structure lying in depth. These spaces are not in the physical optics of the situation, but in the organization of sensory input by the neural system. Such clearly constructed purely synthetic spaces have the same basic quality as the spaces of ordinary experience, and there is a continuous spectrum of spatial experiences between them.

Sensory spaces are not known by direct apperception, but are generated by neural activity coordinated with surrounding physical space. Much of sensation is not experienced at the location of the nerves that support it. This is vividly illustrated by the amputee's experience of the phantom limb. The colors that are induced by the flicker of a strobe seem to be in front of the face, not at the retina or visual cortex. This disparity between the location of a nerve and its sensation indicates that the whole field of a person's sensation is a projection, for there is no difference between the sensation of a nerve stimulated in these unusual ways and one that has been simulated by natural agents.

The topology of the neural network and its events has no necessary resemblance to the topology of the sensory experiences. The physical events in the brain that support sensory or dream space may be highly scattered, but the operations between them give the feeling of contiguity which is spatially convincing. The source of sensory spaces is neural events in physical space, but their geometry is not in physical space.

The union of general sensory space and physical space is the ordinary space experienced in daily life. The familiar world is the union of ordinary space and experience which has location in this space. Dreams and drug deliriums are not in the ordinary external world, but their spaces can be so well developed that the perspective of objects actually changes to correspond with the movements of the observer within them. Hallucinations are false perceptions that appear to be located in ordinary space. Visual afterimages are an interface between visual and physical spaces. They have definite locations in the immediate two-­dimensional visual manifolds, but not in the three-dimensional general sensory space or in physical space.

Conclusion

A manifold is an ordered assemblage of elements each uniquely located by exactly n specific descriptions. Space is a special kind of manifold. Spaces are of many varieties from Poincaré's sensory spaces to ideal mathematical spaces, dream spaces, and hybrid spaces such as general sensory space. Understanding spaces as manifolds clearly shows how spaces can be distorted, and generated, and how sensory and dream spaces can have extension which does not conflict with the extension of physical space.

---

1 J. Piaget, The Origin of Intelligence in the child, Routledge and Kegan Paul, London, 1953. J. Piaget and B Inhelder, The Child's Conception of Space, Routledge and Kegan Paul, London, 1956.

2 M. Von Senden, Space and Sight, trans. P. Heath, Methuen-Free Press, 1960. R.L. Gregory and J.G. Wallace, "Recovery from early blindness: a case study," Exp. Psychol. Soc. Monograph No.2, Cambridge, 1963.

3 Henri Poincaré, Mathematics and Science: Last Essays, Chs. 2 and 3, Dover, New York, 1963.

4 For our purposes, we do not need to consider the problems of higher con nectivities. For example a circle is a one-dimensional manifold of points but two points must be removed to cut it into two parts. Any n dimensional manifold such that the removal of a single n-i dimensional manifold cuts it into two parts is said to be simply connected. The manifolds with which we will be concerned are simply connected.

5 This example is from A. d'Abro, The Evolution of Scientific Thought, Dover, 1950.

6 Given a graded gray wire, the gray and the metal are one-dimensional manifolds, and so is the combination. We need to be mindful of what features we are considering.

7 For example, the visual field is coarser toward the periphery. Another example: two pin pricks on the skin, when very close together, are experienced as a single prick.

8 The distance relation satisfies the following conditions. Let d(P,Q) be the distance between P and Q, then:

d(P,P) = 0, d(P,Q) > 0 if P ≠ Q

d(P,Q) = d(Q,P)

d(P,Q) + d(Q,R) > d(P,R)

9 For example, the immediate visual field is not homogeneous. Visual acuity at the periphery of the visual field is much lower than at the center. The kinesthetic space of arm movements is not isotropic. Extending an arm feels different from moving it sideways.

10 H.H. Price, "Survival and the idea of 'another world"', Proc. Soc. Psychical Research, 1953, pp. 11-12.

11 Poincaré,Mathematics and Science: Last Essays, Ch. 3.

12 Although these operations can generate contiguity and extension in a visual or kinesthetic field, these features of a field are not sufficient for the perceptual unity which is present in consciousness, and the binding problem is not solved.

Read More...

Summary only...